突然始まるユークリッド空間なのだ.
今回は,松坂和夫「集合・位相入門」の142頁の例 ( a ) の証明の行間埋立てをしてみるのだ.
教科書開くのが面倒臭い人のために書いておくと,
- 第4章 位相空間 > B) $\mathbb{E}^n$ の部分集合の内部(開核),外部,境界 > 例 ( a )(142頁)
に書いている話しなのだ.
まずは命題なのだ
$n$ 次元ユークリッド空間 $\mathbb{E}^n$ の部分集合として,開球体 $M=B(a\,;\,\varepsilon)$ が与えられているとする.このとき, $M^i=M$ である.
証明の方針なのだ
$M$ の内部の定義より,$M^i\subseteq M$ であるから,$M^i =M$ であるためには,$M\subseteq M^i$ であればよい.すなわち,任意の $m$ に対して,\[m\in M\Longrightarrow m\in M^i\]を示せばよい.ところで,$m\in M^i$ の定義は,「ある $\varepsilon’>0$( $\varepsilon’\in\mathbb{R}$ )が存在して,\[B(m\,;\,\varepsilon’)\subseteq M\]である」だから,\[x\in B(m\,;\,\varepsilon’)\Longrightarrow x\in M\]を満たす $\varepsilon’$ を構成しよーっと.
↓図はイメージです↓
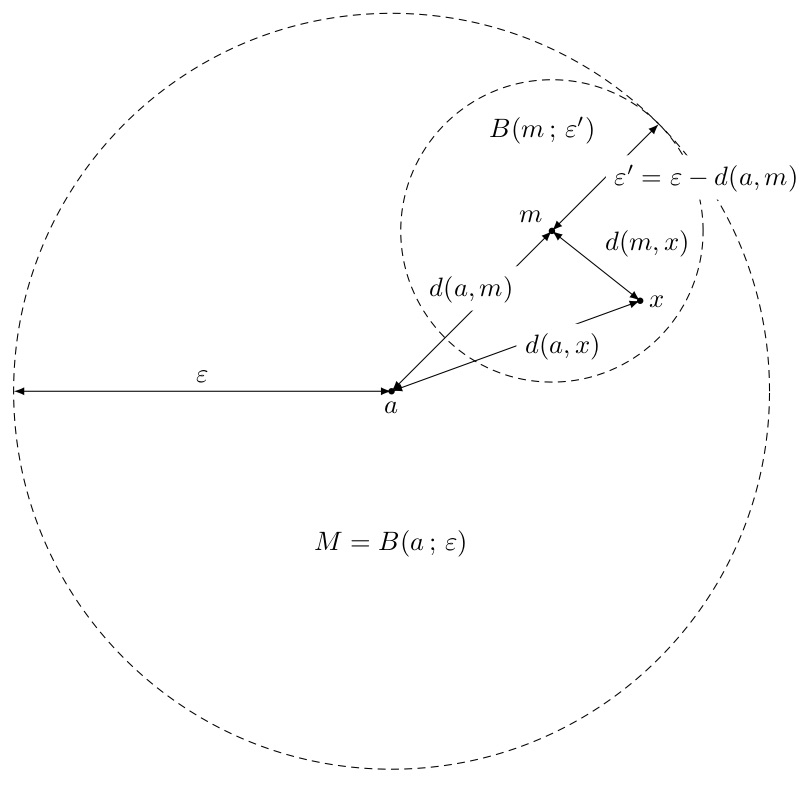
証明するのだ
任意の $m\in M$ に対して,$d(a,m)<\varepsilon$ である.$\varepsilon’$ を\[\varepsilon’=\varepsilon-d(a,m)\]と定めると,$\varepsilon’>0$ である.
任意の $x\in B(m\,;\,\varepsilon’)$ に対して,三角不等式より,
\[d(a,x)\leqq d(a,m)+d(m,x)\]
である.また,$x\in B(m\,;\,\varepsilon’)$ より,$d(m,x)<\varepsilon’$ であるから,
\[d(a,m)+d(m,x)<d(a,m)+\varepsilon’\]
となる.上で $\varepsilon’=\varepsilon-d(a,m)$ と定めたから,
\[d(a,m)+\varepsilon’=\varepsilon\]
である.これらより,
\[d(a,x)<\varepsilon\]
となるから,$x\in B(a\,;\,\varepsilon)$ である.部分集合の定義より,
\[B(m\,;\,\varepsilon’)\subseteq B(a\,;\,\varepsilon)\]
であり,内点の定義より,$m$ は $B(a\,;\,\varepsilon)$ の内点である:$m\in M^i$.
以上より,\[m\in M\Longrightarrow m\in M^i\]である:$M\subseteq M^i$.したがって,$ M^i=M$.
まとめ
松坂本には読んでいて迷子になる部分が所々にあって,今回の証明もそうだったのだ.何をどうすれば証明したことになるのかが書いてなくて,よく事情がわからないまま証明が終わっていることになっていることに少し頭にきたのだ.んで,行間の埋立て工事を施工しましたなのだ.
御査収下さいますよう,よろしく御願い申し上げますなのだ!
いじょ ヽ(´ー`)ノ
ブログ村ランキング参加中
クリック↓してもらえると励みになります.
![]()
にほんブログ村
Amazonにて「素朴集合論」販売中です(Kindle版).製本版は販売休止中スマン.
Views: 923

